Las cuatro nobles verdades

(es) Las cuatro nobles verdades

(eo) La kvar noblaj veraĵoj

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Una vista de Buda sentado en posición de loto.

Motivación:

Un documental sobre las maravillas del mundo budista.

Las cuatro nobles verdades son:

1. Toda existencia es sufrimiento: Nacer es sufrir, enfermar es sufrir, envejecer es sufrir, morir es sufrir, amar es sufrir, perder al ser amado es sufrir, etc. Todo conlleva sufrimiento, la existencia y sus partes son sufrimiento.
2. La causa del sufrimiento es el apego, el deseo.
3. El apego y el deseo pueden suprimirse extinguiendo su causa.
4. El apego y el deseo pueden extinguirse por medio del noble camino óctuple:
   1. Comprensión correcta
   2. Pensamiento correcto
   3. Palabra correcta
   4. Acción correcta
   5. Ocupación correcta
   6. Esfuerzo correcto
   7. Atención correcta
   8. Concentración correcta

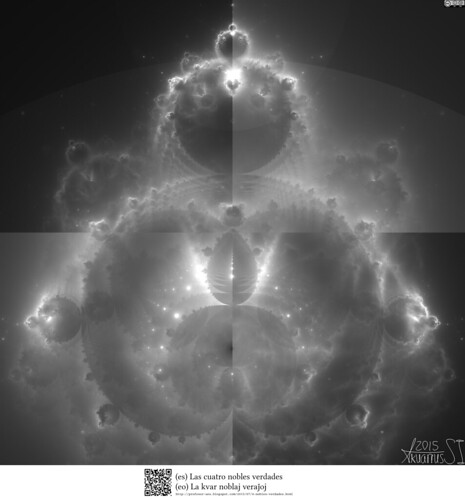
Descripción técnica:

Una vista de alta resolución de un conjunto basado en el de Mándelbrot, conocido como Búdabrot, dibujado con la traza de los puntos de las sucesiones requeridas para determinar la pertenencia de puntos aleatorios $c$ en el conjunto de Mándelbrot. Es decir, se toman puntos complejos $c$ aleatorios. Luego se determina su pertenencia al conjunto de Mándelbrot de la manera estándar:

El conjunto de Mándelbrot es el conjunto $M$ de todos los puntos $c$ del plano complejo tal que la sucesión $z_{n+1}=z_n^2+c$ (con $z_0=0+0i$) no diverge (es decir, tal que es acotada).

El criterio usado para determinar si las sucesiones divergen o no, es si $z_k$, con $k\le N$, tiene un módulo mayor que 2, es decir $\left|z_k\right|⩾2$ (procedimiento estándar para los conjuntos de Julia y de Mándelbrot). Puesto que no puede evaluarse hasta el infinito, se usa una cota: $N$. Si la sucesión no “diverge” antes de llegar al $N$-ésimo término de las sucesiones, se considera que no diverge, es decir que es acotada.

La imagen está dividida en cuatro partes. Las de los “cuadrantes” I y III fue construida haciendo $N=200$ iterando $1,54\times 10^{10}$ puntos aleatorios $c$ del plano complejo. Las de los “cuadrantes” II y IV fue construida haciendo $N=2000$ iterando $3,1\times 10^9$ puntos aleatorios $c$ del plano complejo. En todos los casos $c\in \left[-1.5,0.5\right]\times \left[-1i,1i\right]$.

Archivos

Código parcial (Python):

#!/usr/bin/env python
# coding: utf-8

import math
#import escala
import datetime
from random import uniform
import sys
import os
import subprocess

TAM = 1000
MAXPASOS = 200
NUMPUNTOS = 10000000

LIMITEMODULO = 2.0
LIMITEMODULO2 = 4.0

ANCHO = TAM
ALTO  = TAM

#Mandelbrot en posición usual
SUPERIOR_DER = (0.5, 1.0)
INFERIOR_IZQ = (-1.5,-1.0)


#e = escala.Escala((ANCHO,ALTO), INFERIOR_IZQ, SUPERIOR_DER)

def budabrot(lienzo):
 print "Creando matriz de contadores"
 for i in xrange(TAM):
  L = []
  for j in xrange(TAM):
   L.append(0)
  lienzo.append(L)
 tx = ty = TAM
 
 #Para cantidades grandes de NUMPUNTOS...
 porcentajes = [(x+1)/500.0 for x in range(500)]
 porcentajes.reverse()
 
 print "Iniciando cálculo de puntos"
 print "0%"
 Zx = [0]*MAXPASOS #La secuencia de los pixeles de los puntos que tienden al infinito
 Zy = [0]*MAXPASOS
 for i in xrange(NUMPUNTOS):
  c_r = uniform(INFERIOR_IZQ[0],SUPERIOR_DER[0]) #uniform(e.minxv,e.maxxv)
  c_i = uniform(0.0,SUPERIOR_DER[1]) #uniform(0.0,e.maxyv)
  
  #z = 0 + 0*1j
  z_r = 0.0
  z_i = 0.0
  numPasos = 0
  while numPasos<MAXPASOS and (z_r*z_r+z_i*z_i)<LIMITEMODULO2:
   Zx[numPasos] = int( (z_r - INFERIOR_IZQ[0])*tx/(SUPERIOR_DER[0]-INFERIOR_IZQ[0]) ) #(e.vrx(z_r))
   Zy[numPasos] = int( (z_i - SUPERIOR_DER[1])*ty/(INFERIOR_IZQ[1]-SUPERIOR_DER[1]) ) #(e.vry(z_i))
   
   #z= z*z + c
   z_r_2 = z_r*z_r - z_i*z_i + c_r
   z_i_2 = 2*z_r*z_i + c_i
   z_r = z_r_2
   z_i = z_i_2
   numPasos += 1
  if numPasos<MAXPASOS: #Sí diverge
   while numPasos>0:
   #while numPasos>1: #Esto mejora la imagen
    xZ = Zx[numPasos]
    yZ = Zy[numPasos]
    numPasos -= 1
    if 0 <= xZ and xZ < tx and 0 <= yZ and yZ < ty:
     lienzo[xZ][yZ] += 1 #Aquí se rota la imagen
     lienzo[xZ][ty-yZ-1] += 1
  #print i,",",
  #Para cantidades grandes de NUMPUNTOS...
  if len(porcentajes)>0 and float(i)/NUMPUNTOS>porcentajes[-1]:
   print "{:2.1f}% - {}px-{}-{}".format(porcentajes.pop()*100,TAM, MAXPASOS,NUMPUNTOS)
 print "100%"
 
 print "Calculando máximo"
 maxcuenta = 0
 for Fila in lienzo:
  for n in Fila:
   if n > maxcuenta:
    maxcuenta = n
 return maxcuenta



if __name__ == "__main__":
 global lienzo, maxcuenta
 
 if len(sys.argv)==1:
  print "Se esperaban tres parámetros: TAM ({}), MAXPASOS({}), NUMPUNTOS({})".format(TAM, MAXPASOS,NUMPUNTOS)
  print "Tomando valores por defecto."
 elif len(sys.argv)!=4:
  print "Se esperaban tres parámetros: TAM ({}), MAXPASOS({}), NUMPUNTOS({})".format(TAM, MAXPASOS,NUMPUNTOS)
  print "Respectivamente son:\nla Resolución de la imagen,\nel número de pasos para determinarla convergencia, y\nEl número de puntos aleatorios a generar"
  exit()
 elif len(sys.argv)==4:
  try:
   TAM = int(sys.argv[1])
   MAXPASOS = int(sys.argv[2])
   NUMPUNTOS = long(float(sys.argv[3]))
  except:
   print "Error en los parámetros"
   exit()

 while True: #Debe matarse para terminar
  print "TAM: {}\nMAXPASOS: {}\nNUMPUNTOS: {}".format(TAM, MAXPASOS, NUMPUNTOS)
  
  ini = datetime.datetime.today()
  print "Inicio: {:02}:{:02}:{:02}".format(ini.hour,ini.minute,ini.second)
  lienzo = []
  maxcuenta = budabrot(lienzo)
  fin = datetime.datetime.today()
  
  #guardar en pgm
  nombrearchivo = "budabrot-{}px-{}-{}--{}{:02}{:02}{:02}{:02}{:02}-{}.pgm".format(TAM, MAXPASOS,NUMPUNTOS, fin.year, fin.month, fin.day, fin.hour, fin.minute, fin.second,os.getpid())
  print "Guardando archivo...{}".format(nombrearchivo)
  f = open(nombrearchivo,'w')
  f.write("P2\n{} {}\n{}\n".format(TAM,TAM, maxcuenta))
  for i in xrange(TAM):
   for j in xrange(TAM):
    f.write('{} '.format(lienzo[i][j]))
   f.write('\n')
  f.close()

  #Reporte final:
  print "Inicio: {}-{:02}-{:02} {:02}:{:02}:{:02}".format(ini.year,ini.month,ini.day, ini.hour,ini.minute,ini.second)
  print "Fin: {}-{:02}-{:02} {:02}:{:02}:{:02}".format(fin.year,fin.month,fin.day, fin.hour,fin.minute,fin.second)