Anillo de Fuego

(es) Anillo de fuego

(eo) Fajroringo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un anillo de fuego que emana calor.

Motivación:

Una lectura parcial del libro Indra's Pearls (ISBN: 0 521 35253 3), y curiosidad sobre las transformaciones de Möbius.

Descripción técnica:

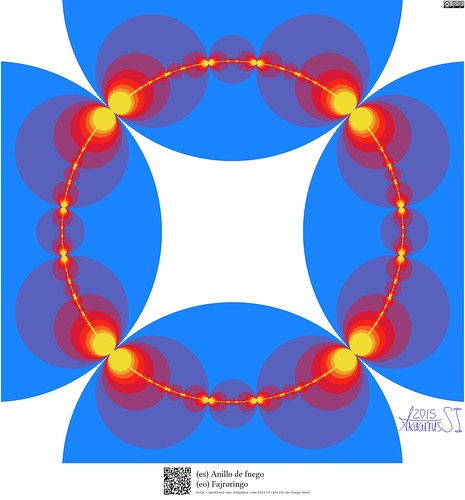
La imagen es una coloración particular de la traza del grupo $\theta$-Schottky con $\theta =\frac{\pi }{4}$ enfatizando su conjunto límite en amarillo intenso.

Los cuatro círculos grandes son los círculos generadores (discos de Schottky). Luego se dibujan las imágenes de cada tres de ellos al interior del cuarto (dadas unas transformaciones de Möbius). Este proceso se repite una y otra vez hasta el infinito. Todos estos círculos se conocen como el grupo de Schottky. Al conjunto de puntos resultantes del proceso (una especie de polvo) se le conoce como El Conjunto Límite del grupo. El conjunto límite del grupo dibujado es exactamente una circunferencia.

El intervalo dibujado es $\left[-1.3,-1.3\right]\times \left[1.3,1.3\right]$.

Archivos

Código (Sage):

# Copyright 2015 Eduardo Adam Navas López
# Este programa es Software Libre liberado bajo la licencia GNU GPLv3 o su versión más reciente:
# http://www.gnu.org/licenses/gpl.html

def grafCircunferencia(c,color=None,z=0,rellena=True):
    """c es una tupla formada por dos elementos:
    c[0]: Un número complejo
    c[1]: Un número real positivo
    """
    if color:
        return circle((real(c[0]),imag(c[0])),c[1],rgbcolor=color,fill=rellena,zorder=z)
    else:
        return circle((real(c[0]),imag(c[0])),c[1])
def mobius_on_point(matriz,punto):
    """matriz: Matriz compleja de 2x2
    punto: Número complejo
    """
    num = matriz[0,0]*punto+matriz[0,1]
    den = matriz[1,0]*punto+matriz[1,1]
    if den == 0:
        return num/(1e-5000)
    else:
        return num/den
def mobius_on_circle(matriz,circunferencia):
    """matriz: Matriz compleja de 2x2
    circunfencia[0]: Número complejo
    circunfencia[1]: Número real positivo
    """
    conjugada = conjugate(matriz[1,1]/matriz[1,0]+circunferencia[0])
    if conjugada == 0:
        z = circunferencia[0] - circunferencia[1]*circunferencia[1]/1e-500000
    else:
        z = circunferencia[0] - circunferencia[1]*circunferencia[1]/conjugada
    nuevoCentro = mobius_on_point(matriz, z)
    nuevoRadio = abs(nuevoCentro - mobius_on_point(matriz, circunferencia[0]+circunferencia[1]))
    return (nuevoCentro, nuevoRadio)
def schottky(generadores, circunferencias, inversos, nivelMax=1,relleno=True):
    """generadores: una lista de 4 matrices complejas de 2x2
    circunferencias: una lista de 4 circunferencias (centro,radio)
    inversos: una lista de 4 números enteros
    nivelesMax: el número de niveles que se desea dibujar (debe ser mayor o igual que 1)
    """
    def definirColor(n):
        "n: nivel actual"
        azul = 25.0/256, 133.0/256, 255.0/256
        rojo = 248.0/256, 7.0/256, 20.0/256
        amarillo = 241.0/256, 221.0/256, 49.0/256
        niv_2 = nivelMax/2.0
        niv = float(nivelMax)
        if n/niv < 0.5:
            return map(lambda i: azul[i]+n*(rojo[i]-azul[i])/niv_2, range(3))
        else:
            return map(lambda i: rojo[i]+(n-niv_2)*(amarillo[i]-rojo[i])/(niv-niv_2), range(3))
    def schottky_aux(g,ixgen,n):
        """g: Generador actual
        ixgen: Índice del generador actual (no puede aplicársele su inversa)
        n: Nivel actual
        """
        graficos = []
        for i in range(4):
            if i!=inversos[ixgen]:
                graficos.append(grafCircunferencia(mobius_on_circle(g,circunferencias[i]),color=definirColor(n),z=n,rellena=relleno))
        if n>=nivelMax:
            return sum(graficos)
        for i in range(4):
            if i!=inversos[ixgen]:
                graficos.append(schottky_aux(g*generadores[i],i,n+1))
        return sum(graficos)
    return sum(map(lambda x: grafCircunferencia(circunferencias[x],color=definirColor(0),z=0,rellena=relleno) + \
                   schottky_aux(generadores[x],x,1), range(4)))
def theta_schottky(theta,niveles,relleno=True):
    P = 1/cos(theta) #sec(theta)
    r = tan(theta)
    Cb = (P,r)
    Ca = (I*P,r)
    CB = (-P,r)
    CA = (-I*P,r)
    b = (1/sin(theta))*matrix([[1,cos(theta)],[cos(theta),1]])
    a = (1/sin(theta))*matrix([[1,I*cos(theta)],[-I*cos(theta),1]])
    A = a**-1
    B = b**-1
    return schottky([b,a,A,B],[Cb,Ca,CA,CB],[3,2,1,0],niveles,relleno)

def graficoSchottky(prueba):
    th=pi/4
    if prueba:
        theta_schottky(th,3).show(figsize=[6,6],xmin=-1.3, xmax=1.3, ymin=-1.3, ymax=1.3,axes=False)
    else:
        print "Generando imagen"
        G = theta_schottky(th,7)
        print "Imagen generada"
        G.show(figsize=[40,40],dpi=200,xmin=-1.3, xmax=1.3, ymin=-1.3, ymax=1.3,axes=False)
        print "Imagen guardada"

graficoSchottky(False)