Inauguración de la exposición de Arte Matemático

Gracias a todas las personas que asistieron.

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Exposición

Del miércoles 30 de marzo al viernes 29 de abril.

Exposición de arte matemático

Por fin conseguí mandar a imprimir mis obras de arte matemático generado por computadora.
Ya conseguí también que me permitan exponerlas en los espacios del CineTeatro y la Pinacoteca de la Universidad. Pero me temo que la agenda de estos espacios ya está llena hasta fin de año, así que se programará mi exposición para el mes de abril del próximo año, aproximadamente del 4 al 25 de abril de 2016.
  

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Torbellinos de pasión

(es) Torbellinos de pasión

(eo) Pasiokirloj

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Dos torbellinos entrelazados girando en la misma dirección.

Motivación:

Una lectura parcial del libro Indra's Pearls (ISBN: 0 521 35253 3), y la búsqueda de comprender las espirales loxodrómicas y los loxódromos en sí (ver Líneas de rumbo).

Descripción técnica:

La imagen es una serie de proyecciones de líneas de rumbo (loxódromos) que se construyen en la esfera de Riemann girada sobre su centro, sobre el plano, por medio de una proyección estereográfica.

El proceso de construcción es el siguiente:

Las líneas de rumbo se inician como espirales exponenciales complejas, de la forma: $T_n\left(z\right)=a^{n}z$, donde $n\in Z$ y $a,z\in C$. Para que las espirales formen una familia como en la imagen, deben tener el mismo valor de $a$. En este caso $a={\displaystyle \frac{4}{5}\left(cos\frac{\pi }{2}+isin\frac{\pi }{2}\right)}$.

Para que estas espirales se conviertan en dobles espirales, se les aplica la siguiente transformación de Möbius

${\hat{T}}_n\left(z\right)=R\circ T_n\circ R^{-1}\left(z\right)$, con $R\left(z\right)=\frac{z-1}{z+1}$

a los números complejos $z$ de la forma $cos\alpha +isin\alpha$, con $\alpha \in \left[\frac{\pi }{4}-0.3,\frac{\pi }{4}+0.3\right]$, y $n\in \{-20,-19,-18,\dots ,29,30\}$.

Nótese que $R\left(0\right)=-1$, $R\left(\infty \right)=1$. Es decir, lo que hace $R$ es tomar un punto del plano complejo, lo proyecta en la esfera de Riemann, luego rota la esfera respecto de su centro (con eje de giro paralelo al eje complejo) y finalmente lo proyecta sobre el plano compleo de nuevo.

Para los colores, se utilizó una técnica de interpolación lineal segmentada pasando por los colores primarios sustractivos (amarillo, cyan y magenta) asociándolos al paso de $\alpha$.

Archivos

Planeta fractal

(es) Planeta fractal

(eo) Fraktalplanedo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un mundo fractal.

Motivación:

Una revisión de las diferentes variantes conocidas de fractales de la familia Mándelbrot.

Descripción técnica:

Una vista de alta resolución de un conjunto fractal similar al de Mándelbrot, pero con ecuación recursiva $z_{n+1}=exp\left(\frac{z_n^2-1,00001z_n}{c^3}\right)$.

El conjunto de Mándelbrot es el conjunto $M$ de todos los puntos $c$ del plano complejo tal que la sucesión $z_{n+1}=z_n^2+c$ (con $z_0=0+0i$) no diverge (es decir, tal que es acotada).

El criterio usado para determinar si las sucesiones divergen o no, es si $z_k$, con $k\le N$, tiene un módulo mayor que 2, es decir $\left|z_k\right|⩾2$ (procedimiento estándar para los conjuntos de Julia y de Mándelbrot). Puesto que no puede evaluarse hasta el infinito, se usa una cota: $N$. Si la sucesión no “diverge” antes de llegar al $N$-ésimo término de las sucesiones, se considera que no diverge, es decir que es acotada.

Archivos

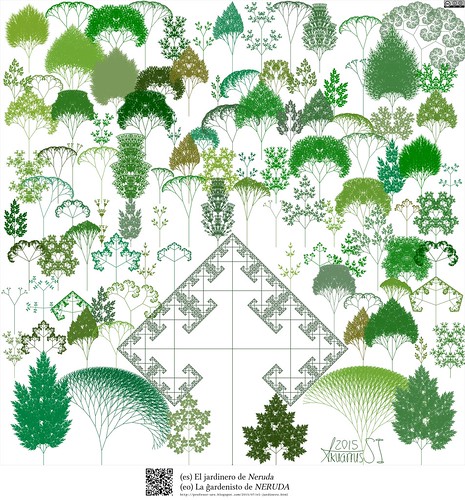
El jardinero de Neruda

(es) El jardinero de Neruda

(eo) La ĝardenisto de NERUDA

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un jardín de plantas fractales rodeando un gran árbol cuadrado que representa una Ceiba.

Motivación:

El recuerdo de un capítulo nunca hecho del libro de Graficación por Computadora del autor... Sería un capítulo sobre fractales biológicos.

Descripción técnica:

Se han utilizado cuatro algoritmos recursivos determinísticos que dibujan “ramas que tienen ramas”. Uno de los algoritmos divide sus ramas en dos ramas, otro divide sus ramas en tres ramas, otro en cuatro y el último en cinco.

Cada árbol depende además de una posición, ángulos de las ramas divididas, tamaño, proporciones entre las ramas y sus ramas hijas, la cantidad de subdivisiones (niveles), posiciones relativas de los brotes de las ramas hijas y el color.

Archivos

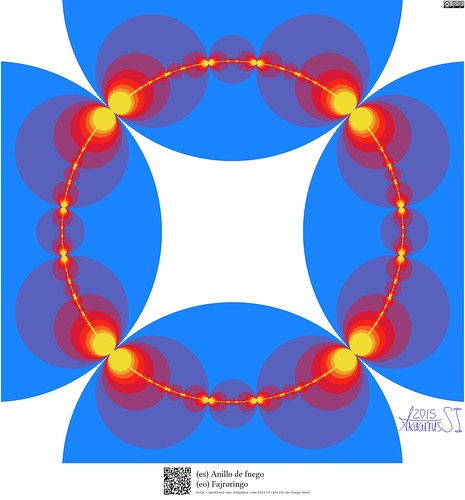
Anillo de Fuego

(es) Anillo de fuego

(eo) Fajroringo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un anillo de fuego que emana calor.

Motivación:

Una lectura parcial del libro Indra's Pearls (ISBN: 0 521 35253 3), y curiosidad sobre las transformaciones de Möbius.

Descripción técnica:

La imagen es una coloración particular de la traza del grupo $\theta$-Schottky con $\theta =\frac{\pi }{4}$ enfatizando su conjunto límite en amarillo intenso.

Los cuatro círculos grandes son los círculos generadores (discos de Schottky). Luego se dibujan las imágenes de cada tres de ellos al interior del cuarto (dadas unas transformaciones de Möbius). Este proceso se repite una y otra vez hasta el infinito. Todos estos círculos se conocen como el grupo de Schottky. Al conjunto de puntos resultantes del proceso (una especie de polvo) se le conoce como El Conjunto Límite del grupo. El conjunto límite del grupo dibujado es exactamente una circunferencia.

El intervalo dibujado es $\left[-1.3,-1.3\right]\times \left[1.3,1.3\right]$.

Archivos

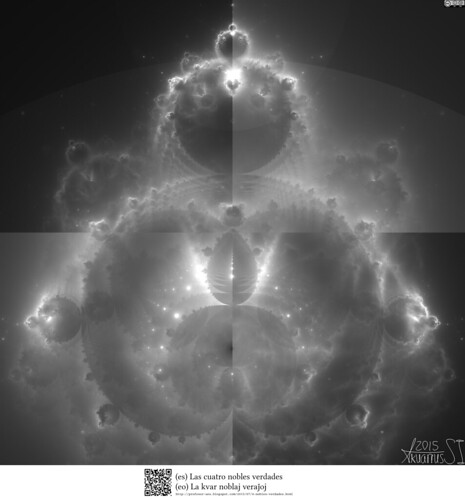
Las cuatro nobles verdades

(es) Las cuatro nobles verdades

(eo) La kvar noblaj veraĵoj

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Una vista de Buda sentado en posición de loto.

Motivación:

Un documental sobre las maravillas del mundo budista.

Las cuatro nobles verdades son:

1. Toda existencia es sufrimiento: Nacer es sufrir, enfermar es sufrir, envejecer es sufrir, morir es sufrir, amar es sufrir, perder al ser amado es sufrir, etc. Todo conlleva sufrimiento, la existencia y sus partes son sufrimiento.
2. La causa del sufrimiento es el apego, el deseo.
3. El apego y el deseo pueden suprimirse extinguiendo su causa.
4. El apego y el deseo pueden extinguirse por medio del noble camino óctuple:
   1. Comprensión correcta
   2. Pensamiento correcto
   3. Palabra correcta
   4. Acción correcta
   5. Ocupación correcta
   6. Esfuerzo correcto
   7. Atención correcta
   8. Concentración correcta

Descripción técnica:

Una vista de alta resolución de un conjunto basado en el de Mándelbrot, conocido como Búdabrot, dibujado con la traza de los puntos de las sucesiones requeridas para determinar la pertenencia de puntos aleatorios $c$ en el conjunto de Mándelbrot. Es decir, se toman puntos complejos $c$ aleatorios. Luego se determina su pertenencia al conjunto de Mándelbrot de la manera estándar:

El conjunto de Mándelbrot es el conjunto $M$ de todos los puntos $c$ del plano complejo tal que la sucesión $z_{n+1}=z_n^2+c$ (con $z_0=0+0i$) no diverge (es decir, tal que es acotada).

El criterio usado para determinar si las sucesiones divergen o no, es si $z_k$, con $k\le N$, tiene un módulo mayor que 2, es decir $\left|z_k\right|⩾2$ (procedimiento estándar para los conjuntos de Julia y de Mándelbrot). Puesto que no puede evaluarse hasta el infinito, se usa una cota: $N$. Si la sucesión no “diverge” antes de llegar al $N$-ésimo término de las sucesiones, se considera que no diverge, es decir que es acotada.

La imagen está dividida en cuatro partes. Las de los “cuadrantes” I y III fue construida haciendo $N=200$ iterando $1,54\times 10^{10}$ puntos aleatorios $c$ del plano complejo. Las de los “cuadrantes” II y IV fue construida haciendo $N=2000$ iterando $3,1\times 10^9$ puntos aleatorios $c$ del plano complejo. En todos los casos $c\in \left[-1.5,0.5\right]\times \left[-1i,1i\right]$.

Archivos

San Romero estudiante

(es) San Romero estudiante

(eo) Sankta Romero studento

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Una fotografía de Óscar Arnulfo Romero y Galdámez en su época de estudiante/seminarista.

Motivación:

La noticia de confirmación de canonización de San Romero de América.

Descripción técnica:

Una fotografía de Óscar Arnulfo Romero y Galdámez que en lugar de estar formada por pixeles (cuadrados) está formada por una teselación rombitrihexagonal.

Archivos

Miel hiperbólica

(es) Miel hiperbólica

(eo) Hiperbola mielo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

 Descripción artística:

Un acercamiento de un panal de miel.

Motivación:

Lectura de un artículo sobre geometría hiperbólica y otra lectura sobre teselaciones.

Descripción técnica:

Una teselación hexagonal de fondo y en frente una teselación hexagonal en geometría hiperbólica proyectada sobre el disco de Poincaré.

Archivos

Las mariposas de El Mozote

(es) Las mariposas de El Mozote

(eo) Papilioj de El Mozote

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Las mariposas del perdón revoloteando en el cielo azul con nubes blancas.

Motivación:

Un capítulo de la amarga historia de nuestro querido El Salvador.

Descripción técnica:

Se han dibujado una serie de mariposas –con la ecuación polar $m\left(\theta \right)=e^{cos\theta }-2cos\left(4\theta \right)+{\left(sin\frac{\theta }{12}\right)}^5$, con $0\le \theta \le 10\pi$– sobre una nube generada por un algoritmo recursivo probabilístico.

Archivos

Homenaje al Doctor Alberto Sánchez

(es) Homenaje al Doctor Alberto Sánchez

(eo) Omaĝo al Doktoro Alberto Sánchez

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Homenaje al Doctor Alberto Sánchez, salvadoreño, quien descubrió el trazo de la curva Cornoide en 1895.

Motivación:

El trabajo de un salvadoreño que aportó la identificación de una curva de construcción relativamente simple que todos los grandes matemáticos de la historia pasaron por alto. La Escuela de Matemática de la Facultad de Ciencias Naturales y Matemática de la Universidad de El Salvador, lleva su nombre en su honor.

Descripción técnica:

Una vieja fotografía del Doctor Alberto Sánchez en la que cada pixel fue cambiado por una pequeña curva Cornoide con más o menos pasos intermedios con colores rojo, azul y verde para provocar los puntos correspondientes en una escala mayor.

Archivos

Construcción de la Cornoide

(es) Construcción de la Cornoide

(eo) Konstruado de Kornokurbo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Instrucciones visuales para el trazo de la curva Cornoide, descubierta por el Doctor Alberto Sánchez, salvadoreño, en 1895.

La secuencia está en espiral: Comenzando en la esquina superior izquierda, luego a la derecha hasta la esquina superior derecha, luego hacia abajo hasta la esquina inferior derecha, luego a la izquierda y así sucesivamente.

Motivación:

Las instrucciones simples pero poco conocidas para la construcción de la Cornoide.

Descripción técnica:

El trazo de la curva Cornoide, en 16 pasos en espiral de afuera hacia adentro.

El procedimiento geométrico para construirla es el siguiente:

Sea $C$ un punto de la circunferencia de diámetro director $AB$ y sea $C\text{'}$ el punto de intersección de la circunferencia con la paralela por el punto $C$ al diámetro $AB$. Desde $C$ se traza la recta tangente a la circunferencia y desde $C\text{'}$ la recta perpendicular a la recta tangente. Sea $D$ el punto intersección de ambas rectas. Cuando el punto $C$ describe la circunferencia, el punto $D$ describe la Cornoide.

Archivos

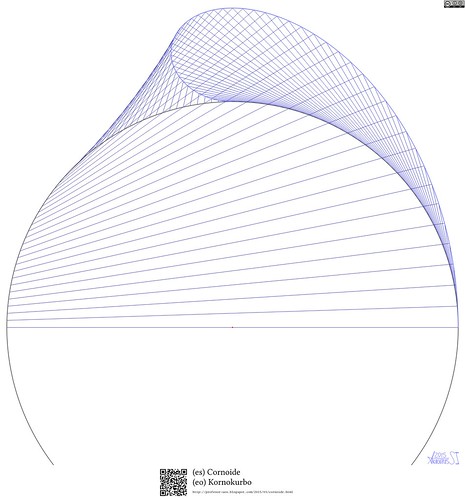
Cornoide

(es) Coronoide

(eo) Kornokurbo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

El trazo de la curva Cornoide, descubierta por el Doctor Alberto Sánchez, salvadoreño, en 1895.

Motivación:

El trabajo de un salvadoreño que aportó la identificación de una curva de construcción relativamente simple que todos los grandes matemáticos de la historia pasaron por alto. La Escuela de Matemática de la Facultad de Ciencias Naturales y Matemática de la Universidad de El Salvador, lleva su nombre en su honor.

Descripción técnica:

El trazo de la curva Cornoide, con ecuación paramétrica:

$\{\begin{array}{cc}x\left(t\right)=R\cdot cost\cdot cos2t& \\ y\left(t\right)=R\cdot sint\cdot \left(2+cos2t\right)& \end{array}$

El procedimiento geométrico para construirla es el siguiente:

Sea $C$ un punto de la circunferencia de diámetro director $AB$ y sea $C\text{'}$ el punto de intersección de la circunferencia con la paralela por el punto $C$ al diámetro $AB$. Desde $C$ se traza la recta tangente a la circunferencia y desde $C\text{'}$ la recta perpendicular a la recta tangente. Sea $D$ el punto intersección de ambas rectas. Cuando el punto $C$ describe la circunferencia, el punto $D$ describe la Cornoide.
Archivos

El desfile de los primos

(es) El desfile de los primos

(eo) Primoparado

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Los números primos desfilando al rededor del número uno.

Motivación:

Una lectura sobre la Esprial de Ullam y sus curiosidades.

Descripción técnica:

Es una espiral cuadrada de cien vueltas con los números primos resaltados. El numero uno se ha marcado con rojo.

Esta construcción se conoce como la Espiral de Ullam.

Archivos

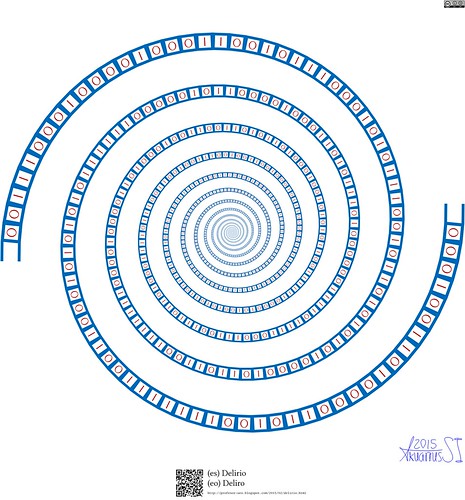
Delirio

(es) Delirio

(eo) Deliro

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Una espiral formada por la cinta enrrollada de una Máquina de Turing binaria. En el centro de la imagen está el motor de la máquina.

Motivación:

Los recuerdos del curso de Teoría Matemática de la Computación.

Descripción técnica:

Dos espirales exponenciales entrelazadas con ecuaciones $r=\pm {\left(\frac{11}{10}\right)}^{\theta }$, con $0\le \theta \le 20\pi$. Cada celda contiene un bit y tiene igual probabilidad de ser uno o cero.

Archivos

La batalla de Esmolensco

(es) La batalla de Esmolensco

(eo) La batalo de Smolensko

(be) Смаленская бітва

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un baño de sangre sobre el suelo helado de Esmolensko (Смаленск).

Motivación:

Una serie de documentales sobre la Segunda Guerra Mundial, particularmente sobre la Operación Barbarroja y cómo se desarrollaron los hechos del avance alemán en suelo soviético en el período de 1941-1943.

Descripción técnica:

Una vista de un conjunto de Julia con semilla $c=0.39-0.252857i$ en el intervalo de los reales: [-0.21,0.63] y en los imaginarios: [-0.865714,-0.025714].

El conjunto de Julia con semilla $c$ es el conjunto $J_c$ de todos los puntos $z$ del plano complejo tal que la sucesión $z_{n+1}=z_n^2+c$ (con $z_0=z$) diverge (o más pragmáticamente tal que es no acotada).

El criterio usado para determinar si las sucesiones divergen o no, es si $z_k$, con $k\le N$, tiene un módulo mayor que 2, es decir $\left|z_k\right|⩾2$ (procedimiento estándar para los conjuntos de Julia y de Mándelbrot). Puesto que no puede evaluarse hasta el infinito, se usa una cota: $N$. Si la sucesión no “diverge” antes de llegar al $N$-ésimo término de las sucesiones, se considera que no diverge, es decir que es acotada.

La coloración de esta obra son puntos de tono rojo y brillo máximo con saturación más baja para los puntos mientras más rápido se determine que no pertenecen al conjunto, y más alta mientras más se tarde en determinar la no pertenencia. Los puntos que sí pertenecen al conjunto se pintan como rojo intenso.

Archivos

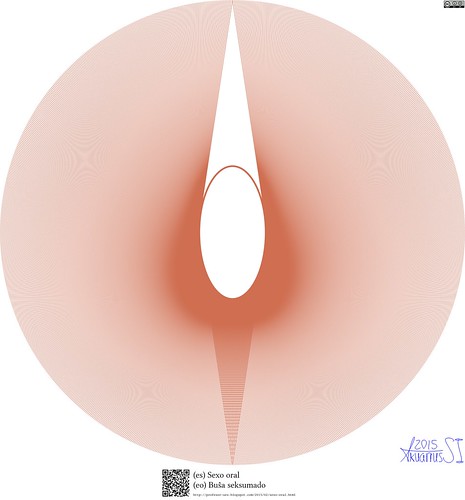
Sexo oral

(es) Sexo oral

(eo) Buŝa seksumado

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Una vista de cunnilingus.

Motivación:

Ver el nombre.

Descripción técnica:

Una serie segmentos de rectas tangentes a la elipse $x^2+\frac{y^2}{2}=1$ que pasan por la circunferencia $x^2+y^2=49$, más el dibujo de la elipse.

Archivos

El baile de los primos

(es) El baile de los primos

(eo) Primobalo

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Los números primos danzando junto con los números compuestos al rededor del número uno.

Motivación:

Una lectura sobre la Esprial de Sacks y sus curiosidades.

Descripción técnica:

Es una espiral polar de la forma $\left(r\left(\rho \right),\theta \left(\rho \right)\right)$, con $\theta =\sqrt{\rho }$, y $r=\sqrt{\rho }$, con $1\le \rho \le 10000$, $\rho \in N$ y $\theta$ medido en revoluciones. Para cada $\rho$ se dibujó un círculo de color negro si es primo y griz si es compuesto.

Esta construcción se conoce como la Espiral de Sacks.

Alineaciones libres de números primos:

• Semirrecta horizontal derecha: cuadrados perfectos.
• Línea inmediatamente inferior a la anterior: números de la forma $n^2-1$, divisibles siempre por $n+1$ y $n-1$.
• Semirrecta horizontal izquierda: números de la forma $n^2+n$, divisibles siempre por $n$ y $n+1$.

Curvas aparentemente densas en números primos:

• Una espiral que, en la ilustración, termina cerca de la parte inferior del disco: números de la forma $n^2+n+41$, el polinomio descubierto por Euler.
• Otra espiral situada varios lugares por encima de la anterior: números de la forma $n^2+n+17$.
• Línea inmediatamente superior a la semirrecta horizontal izquierda: números de la forma $n^2+n-1$.

Archivos

Proyección ortogonal del cubo RGB

(es) Proyección ortogonal del cubo RGB

(eo) Orta projekcio de la kubo RGB

http://dx.doi.org/10.13140/RG.2.2.34092.90243

Descripción artística:

Un cubo hecho de cubitos de los colores brillantes del arcoiris.

Motivación:

Fue una de las primeras ideas de experimento del autor aprendiendo el lenguaje CFDG aunque su concreción requirió más madurez y más experiencia en el lenguaje.

Descripción técnica:

Es la vista clara del cubo de color RGB, proyectado ortogonalmente.

El modelo de color RGB (Red-Green-Blue) es el modelo de colores aditivos más usado y usado en las pantallas emisoras de luz (monitores de computadora, televisores, teléfonos, etc.).

En este modelo los colores están determinados por su combinación de luz roja, luz verde y luz azul. La combinación máxima de los tres tipos de luz produce el color blanco. La ausencia de los tres tipos de luz produce el color negro.

Archivos

Código (CFDG):

# Copyright 2015 Eduardo Adam Navas López
# Este archivo es Software Libre liberado bajo la licencia GNU GPLv3 o su versión más reciente:
# http://www.gnu.org/licenses/gpl.html

#Para generar la imagen:
#$ cfdg -b 0 -s 8000 rgb.cfdg rgb.png

#Número de hexágonos de radio
RADIO = 64 #16

startshape cubo

PORCENTAJE_ESPACIO = 1.1
const1_r3 = (1/sqrt(3))
MEDIOANCHO = (sqrt(3)/2)*PORCENTAJE_ESPACIO
MEDIOALTO = 0.5*PORCENTAJE_ESPACIO
SATMIN = 0.01

shape prueba{
 hexagono1[]
 hexagono2[]
 hexagono3[]
}

shape cubo {
 loop bloque = 3 [r 120]{
  loop anillo = RADIO []{
   loop i = (anillo+1) []{
    loop j = (anillo+1) []{
     px = (i*MEDIOANCHO-j*MEDIOANCHO)
     py = (MEDIOALTO*(i+j))
     hexagono1[x px y py b 1
     sat ((1-SATMIN)*max(i,j)/(RADIO-1)+SATMIN)
     h (atan2(py,px)-30+bloque*120) ]
    }
   }
  }
 }
}

shape dosTriangulos {
  loop i = 2 [r 60]{
   TRIANGLE[y const1_r3 r 180]
  }
}

shape hexagono1 {
 dosTriangulos[r -30]
}

shape hexagono2 {
 dosTriangulos[r 90]
}

shape hexagono3 {
 dosTriangulos[r 210]
}